Treap 期望复杂度的证明

实际上 Treap 的复杂度取决于它的高度…… 那么下面先求一下每个结点的期望高度。

不过要先做一些约定：

  • 结点的高度：根节点高度为 00，否则该结点的高度等于它父亲的高度 +1+1.
  • 树的高度：树中结点的高度的最大值。
  • 这棵 Treap 的优先级（priority）满足：
    • 小根堆性质；
    • 从一个均匀分布中取得。
  • 树的结点总数为 nn，其中第 ii 大的结点直接用它的编号 ii 表示。
  • 随机变量 XX 的期望记作 EX\mathbb{E}X，事件 EE 发生的概率为 Pr⁡(E)\Pr(E).

Treap 结点的期望高度

现在来求一个结点 xx 的期望高度吧。

首先，可以知道的是 xx 的期望高度和它祖先的数量是相等的。因此我们引入一个（一组？）指示器随机变量（indicator random variable） Ai,jA_{i,j} 指示（indicates）事件「结点 ii 是结点 jj 的祖先」，即当 ii 是 jj 的祖先时 Ai,j=1A_{i,j}=1，否则 Ai,j=0A_{i,j}=0. 特别地，我们约定 Ax,x=0A_{x,x}=0，即 xx 不是它自己的祖先。所以结点 xx 的高度

dep(x)=∑i=1nAi,x\text{dep}(x)=\sum_{i=1}^nA_{i,x}

那么它的期望就是

E(dep(x))=E(∑i=1nAi,x)\mathbb E\left(\text{dep}(x)\right)=\mathbb E\left(\sum_{i=1}^nA_{i,x}\right)

而根据期望的线性性 不可以性性！，有

E(dep(x))=∑i=1nEAi,x=∑i=1nPr⁡(Ai,x=1)\begin{aligned} \mathbb E\left(\text{dep}(x)\right)&=\sum_{i=1}^n\mathbb EA_{i,x}=\sum_{i=1}^n\Pr(A_{i,x}=1) \end{aligned}

因此现在需要做的就是求出 Ai,x=1A_{i,x}=1 的概率了，即求出任意一个点是当前结点的祖先的概率。这就需要用到 Treap 优先级的性质了。

于是我们首先证明一个引理：

Ai,j=1  ⟺  priority(i)=min⁡k=ijpriority(k)A_{i,j}=1 \iff \text{priority}(i)=\min_{k=i}^j \text{priority}(k)

Proof. 对于结点 i,ji,j 的位置关系，我们分几类进行讨论。

  1. ii 是 jj 的祖先。
    此时根据小根堆的性质，有 priority(i)<priority(k)\text{priority}(i)<\text{priority}(k) 对于所有的 i<k≤ji<k\le j. 因此充要性成立。
  2. jj 是 ii 的祖先。
    此时同样根据小根堆的性质，有 priority(j)>priority(i)\text{priority}(j)>\text{priority}(i). 因此充要性仍然成立。
  3. 对于根节点而言，ii 和 jj 在两棵不同的子树上。
    此时由于二叉搜索树的性质，显然他们的 LCA 介于他们之间，即 i<LCA(i,j)<ji<\text{LCA}(i,j)<j. 因此如果取 k=LCA(i,j)k=\text{LCA}(i,j)，同样由小根堆性质推出 priority(k)>priority(i)\text{priority}(k)>\text{priority}(i)，充要性仍然成立。
  4. i,ji,j 在根节点的同一个子树上。
    此时如果将这个子树（不管是左子树还是右子树都一样）单独拎出来看，会发现它也是一棵 Treap。因此我们直接递归地重复上面的证明即可。□\square

证完引理，那么接下来的问题就不大了。由于此时 Ai,x=1A_{i,x}=1 的概率等于 ii 的优先级是 [i,x][i,x] 区间中所有结点中最小的那个。而由于优先级是取自一个均匀分布，因此 [i,x][i,x] 中任何一个结点的优先级恰好是最小的概率都相等，即为 1∣x−i+1∣\dfrac{1}{|x-i+1|}（不过有特殊情况 Ax,x≡0A_{x,x}\equiv 0！因此求和的时候要挖掉这个点） 因此直接代入计算即可：

E(dep(x))=∑i=1nPr⁡(Ai,x=1)=∑i=1x−11x−i+1+∑i=x+1n1i−x+1=∑j=2x1j+∑j=2n−x+11j\begin{aligned} \mathbb E(\text{dep}(x))&=\sum_{i=1}^n\Pr(A_{i,x}=1)\\ &=\sum_{i=1}^{x-1}\dfrac 1{x-i+1}+\sum_{i=x+1}^n\dfrac 1{i-x+1}\\ &=\sum_{j=2}^x \dfrac 1j+\sum_{j=2}^{n-x+1}\dfrac 1j \end{aligned}

然后做一个大胆的放缩：直接让求和的上界放大到 nn，也就是

E(dep(x))<2∑j=2n1j\mathbb E(\text{dep}(x))< 2\sum_{j=2}^n\dfrac 1j

然后我们考虑如何求这一堆倒数和。再做一次放缩，把倒数 1j\dfrac 1j 放大成积分 ∫j−1j1xdx\displaystyle \int_{j-1}^j\dfrac 1x\text dx：

E(dep(x))<2∑j=2n1j<2∑j=2n∫j−1j1xdx=2∫1n1xdx=2ln⁡n=O(log⁡n)\begin{aligned} \mathbb E(\text{dep}(x))&< 2\sum_{j=2}^n\dfrac 1j\\ &<2\sum_{j=2}^n\int_{j-1}^j\dfrac 1x\text dx\\ &=2\int_1^n\dfrac 1x\text dx\\ &=2\ln n=O(\log n) \end{aligned}

因此，对于 Treap 中的每一个节点，它的期望深度都是 O(log⁡n)O(\log n).

另一种证明方法 在进行最后一次放缩（即放大成积分）之前，我们注意到需要处理的和式恰好是一个调和数，即

E(dep(x))<2∑j=2n1j=2Hn−2<2Hn\mathbb E(\text{dep}(x))< 2\sum_{j=2}^n\dfrac 1j=2H_n-2<2H_n

而对于调和数来说，根据不等式

12(n+1)<Hn−ln⁡n−γ<12n\dfrac 1{2(n+1)}<H_n-\ln n-\gamma<\dfrac 1{2n}

(Young 1991; Havil 2003, pp. 73-75)，其中 γ≈0.577\gamma\approx 0.577 是 Euler-Mascheroni 常数。因此 Hn=O(log⁡n)H_n=O(\log n) 应当是比较显然的。

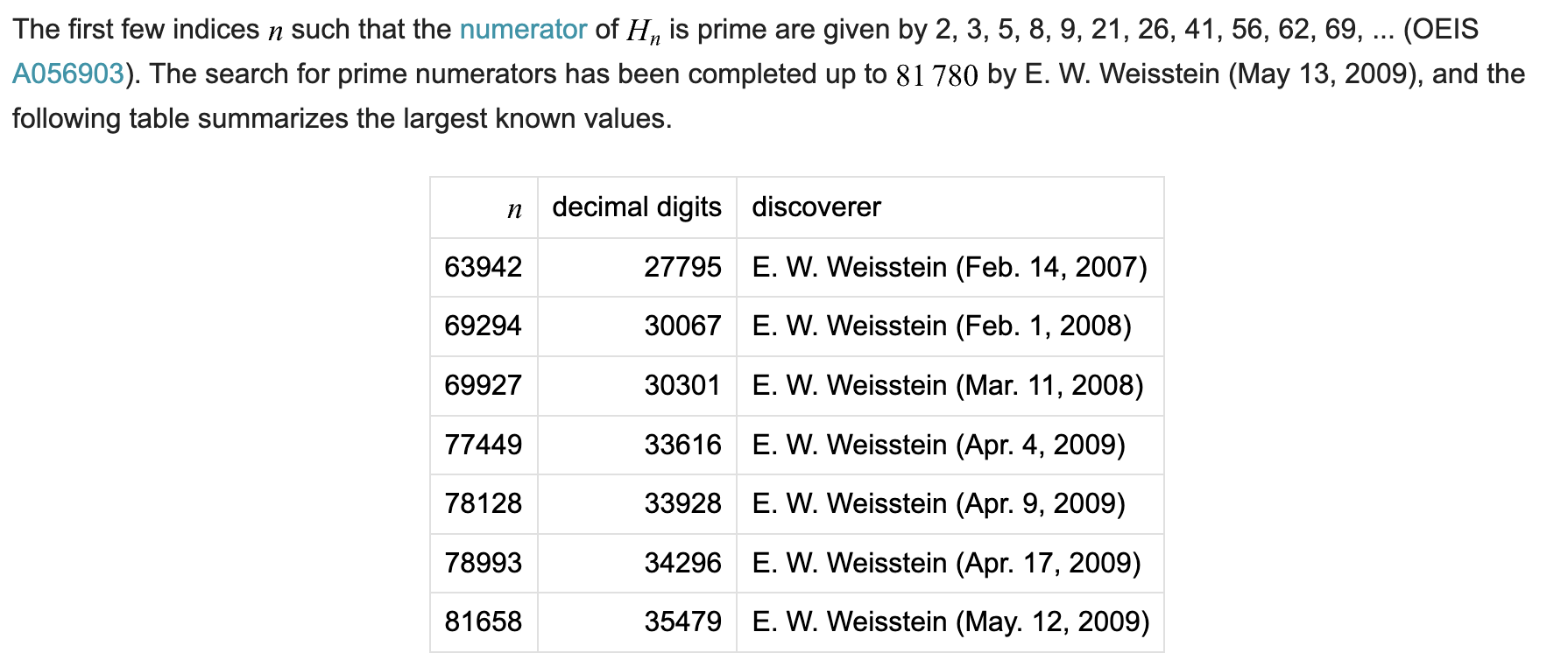
题外话：查 HnH_n 性质的时候发现的。Weisstein 你是真的闲啊（

白石头.png

白石头.png

操作的复杂度

嗯结点期望高度搞出来之后别的应该就比较显然了吧？

众所周知二叉搜索树的各个操作都应当是 O(h)O(h) 的（其中 hh 是树高），因此查询前后继、查排名、排名查值这些不改变树结构（因此不需要额外的维护操作）的操作也是期望 O(h)=O(log⁡n)O(h)=O(\log n) 的。

那么现在需要解决的就是插入和删除了。

根据二叉堆的结论，如果一个结点违反了堆性质（要么和父亲违反，要么和儿子违反），需要的调整次数只和这个点的深度相关。

如果和父亲违反（需要 shiftUp）则需要最坏 dep(x)<h\text{dep}(x)<h 次调整（调到树根）；如果和儿子违反（需要 shiftDown）则是最坏 h−dep(x)<hh-\text{dep}(x)<h 次（调到叶子，并且这个叶子还是最深的那个）。

考虑最深的那个叶子，由于它的期望高度也是 O(log⁡n)O(\log n)，因此整棵树的期望高度也是 O(log⁡n)O(\log n). 所以上面插入和删除后，维护 Treap 性质时需要的调整次数的期望也是 O(log⁡n)O(\log n). 因此插入和删除的总复杂度的期望也是 O(log⁡n)O(\log n).